How to Use Log on a Calculator

How to Use Log on a Calculator | Step-by-Step Guide with Examples and Explanation

by

Introduction: What is a Logarithm, and Why is It Important?

A logarithm is a fundamental mathematical concept used to solve equations involving exponential growth or decay. It’s the inverse operation of exponentiation, meaning it answers the question: To what power must a number (called the base) be raised to obtain a certain value?

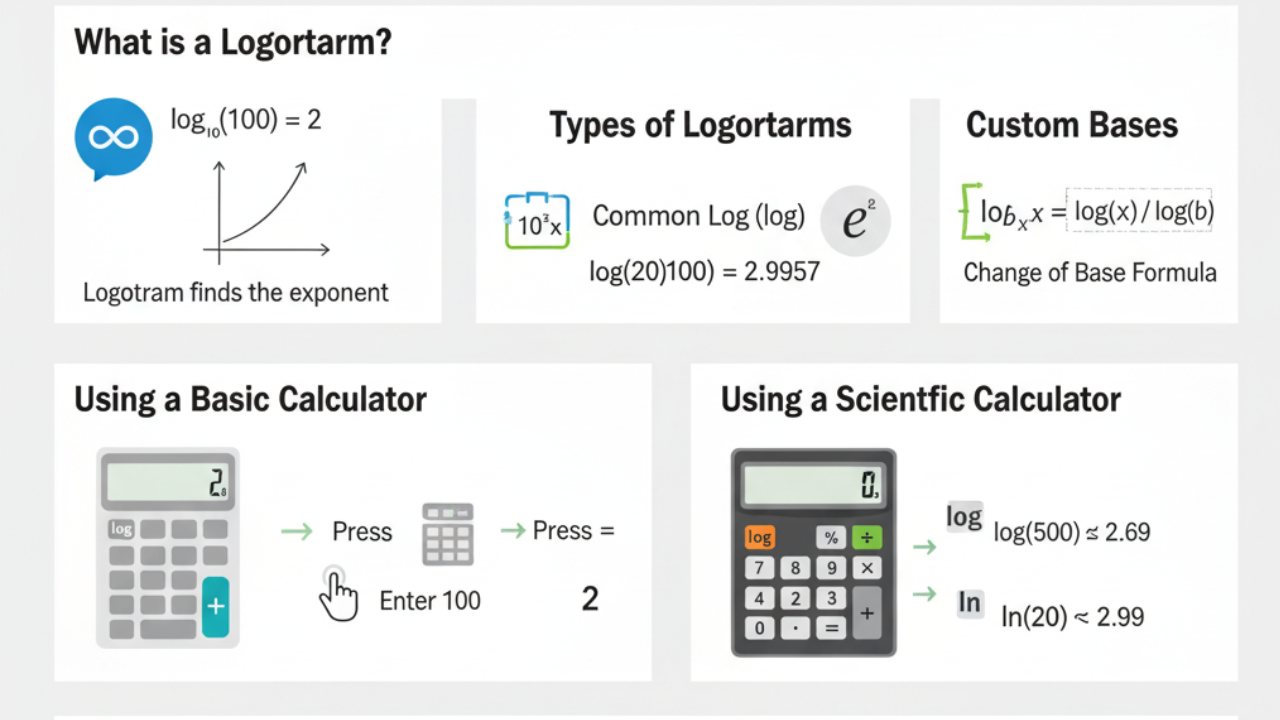
For instance, if you want to solve for log base 10 of 100, written as log10(100), you are essentially asking, “What power must 10 be raised to get 100?” The answer is 2, because 10^2 = 100. So, log10(100) = 2.

Understanding how to use a logarithmic function on a calculator is essential for efficiently performing these calculations, especially when working with logarithms base 10 (common logarithms) and natural logarithms (ln). Logarithms are used in a wide variety of fields, from finance and engineering to science and computer programming.

In this guide, we will cover:

  1. How to use a log on both basic and scientific calculators.

  2. Different types of logarithms.

  3. Practical uses and applications of logarithms.

  4. Common mistakes to avoid when using logs on a calculator.

By the end of this guide, you will be equipped to confidently use logarithmic functions on a calculator for different scenarios.

 What is a Logarithm?

A logarithm answers the question, “To what power must a number (the base) be raised to produce a given number?”

  • Common Logarithm (log): Base 10 (log base 10), written as log(x)</>.
  • Natural Logarithm (ln): Base e (~2.718), written as ln(x)</>.

For example log(100) = 2, because 10 raised to the power of 2 equals 100. Similarly, it ln(20) would be calculated using base e.

What Are the Different Types of Logarithms?

Common Logarithms (log)

The most common type of logarithm is the common logarithm, or log base 10. When you use the log button on a calculator, you are usually calculating a logarithm with base 10. The common logarithm is used extensively in science, engineering, and finance.

  • Example: log⁡10100=2\log_{10} 100 = 2 because 102=10010^2 = 100.

Natural Logarithms (ln)

The natural logarithm uses base e (approximately 2.718), and it’s denoted as ln(x). The natural log is frequently used in calculus, physics, and other advanced fields of mathematics.

  • Example: ln⁡(20)\ln(20) uses the base e, and this is often used in calculations involving exponential growth, decay, and compound interest.

Logarithms with Custom Bases

Some scientific calculators allow you to calculate logarithms with bases other than 10 or e, such as log base 2 (which is often used in computer science) or other values.

How to Use a Log on a Basic Calculator

Step 1: Locate the Log Button

Most basic calculators have a log button that calculates the common logarithm (base 10). This is ideal for calculating logarithms with base 10, which is the most commonly used logarithmic function.

Step 2: Input the Number

After pressing the log button, you can input the number you want to find the logarithm of. For example, if you want to calculate log⁡10100\log_{10} 100, you would:

  1. Press the log button.

  2. Enter the number 100.

Step 3: Press Equals

After entering the number, press the equals button (=) to calculate the logarithmic value. In this case, the result will be 2, because 102=10010^2 = 100.

Example:

  • Log Calculation: To find log⁡10100\log_{10} 100, press:
  • log, enter 100, press =.
  • Result: 2.

How to Use a Log on a Scientific Calculator

Scientific calculators are more advanced and allow you to calculate both common logarithms (log) and natural logarithms (ln). Here’s how to use the log function on a scientific calculator:

Step 1: Set the Calculator to Log Mode

For log base 10, press the log button. For natural logarithms (ln), press the ln button. Ensure you’re in the correct mode for the type of logarithm you want to calculate.

Step 2: Enter the Number

After pressing the appropriate button (log or ln), input the number you want to calculate the logarithm for.

  • To calculate log⁡10500\log_{10} 500, press log and then enter 500.

  • To calculate ln⁡(20)\ln(20), press ln and then enter 20.

Step 3: Press Equals

Once you’ve entered the number, press the equals button (=). The calculator will display the result.

Example:

  • Log Base 10: To calculate log⁡10500\log_{10} 500, press:

    • log, enter 500, press =.

    • Result: 2.69897 (approximately).

  • Natural Log (ln): To calculate ln⁡(20)\ln(20), press:

    • ln, enter 20, press =.

    • Result: 2.9957 (approximately).

How to Use Custom Bases for Logarithms

How to Use Log on a Calculator
How to Use Log on a Calculator

If you need to calculate logarithms with custom bases (like log base 2 or log base 5), use the change of base formula:

log_b(x) = log(x) / log(b)

Where:

  • b is the base (e.g., 2 or 5)

  • x is the number you’re calculating the logarithm for

For example, to calculate log_2(16)</>:

  1. Use the change of base formula: log_2(16) = log(16) / log(2)
  2. Calculate the values: log(16) = 1.204, log(2) = 0.301
  3. Divide: 1.204 / 0.301 = 4

Thus, log_2(16) = 4 because 2^4 = 16.

Practical Applications of Logarithms

Logarithms in Finance

In finance, logarithms are often used to calculate compound interest, loan growth, and exponential returns. For example, the compound interest formula:

A = P * (1 + (r/n) * t)

Where:

  • A is the future value

  • P is the principal amount

  • r is the annual interest rate

  • n is the number of times interest is compounded annually

  • t is the time in years

Logarithms in Science

In science, logarithms are used to model decay rates, pH levels, and sound intensity.

  • For example, pH is the negative logarithm of the concentration of hydrogen ions:

                                          pH = -log[H+]

Common Mistakes to Avoid When Using a Log on a Calculator

  • Wrong Base: Make sure you’re using the correct logarithmic function (log for base 10, ln for base e).

  • Incorrect Input: Double-check the numbers you input. Logarithms can only be calculated for positive values.

  • Confusing Logarithms with Exponentiation: Remember that logarithms are the inverse of exponentiation. For example, log⁡10100=2\log_{10} 100 = 2, not 102=10010^2 = 100.

Frequently Asked Questions (FAQs)

Q1: How do I use a log on a calculator?

A1: To use log on a calculator, press the log or ln button, input the number, and press equals. For common logs, use log (base 10), and for natural logs, use ln (base e).

Q2: What is the difference between log and ln?

A2: log refers to the logarithm with base 10, while ln refers to the logarithm with base e (approximately 2.718).

Q3: Can I calculate logarithms with custom bases on my calculator?

A3: Yes, you can use the change of base formula to calculate logarithms with custom bases, such as base 2 or base 5.

Q4: How do I calculate log base 2 on a calculator?

A4: Use the change of base formula: log_b(x) = log(x) / log(b)

7. Conclusion: Mastering Logarithms on Your Calculator

Using the logarithmic function on a calculator is a valuable skill for simplifying complex calculations in math, science, and finance. By understanding how to use log base 10 and natural logs effectively, you can solve a wide variety of equations and perform accurate, efficient calculations.

Leave a Comment