Introduction
Calculating the square root without a calculator is easier than you think. Whether you’re tackling a math exam or just want to sharpen your mental math skills, knowing how to find the square root manually is a useful skill.
In this guide, we’ll show you how to find square roots using easy methods like estimation, long division, and the Babylonian method, which you can apply to both small and large numbers.
Why Learn to Find Square Roots Without a Calculator?
1. Improve Mental Math Skills
By practicing how to find square roots without a calculator, you’ll strengthen your number sense and improve mental math. This can make solving math problems in exams or everyday life much faster and easier.
2. Practical Use
Square roots appear in various subjects such as geometry, physics, and engineering. Whether you’re solving problems in school or during daily tasks, finding square roots without a calculator can come in handy.
3. Understand the Concept
Understanding how to calculate square roots manually also deepens your understanding of mathematics. It’s not just about memorizing answers, but about grasping the underlying principles behind the numbers.
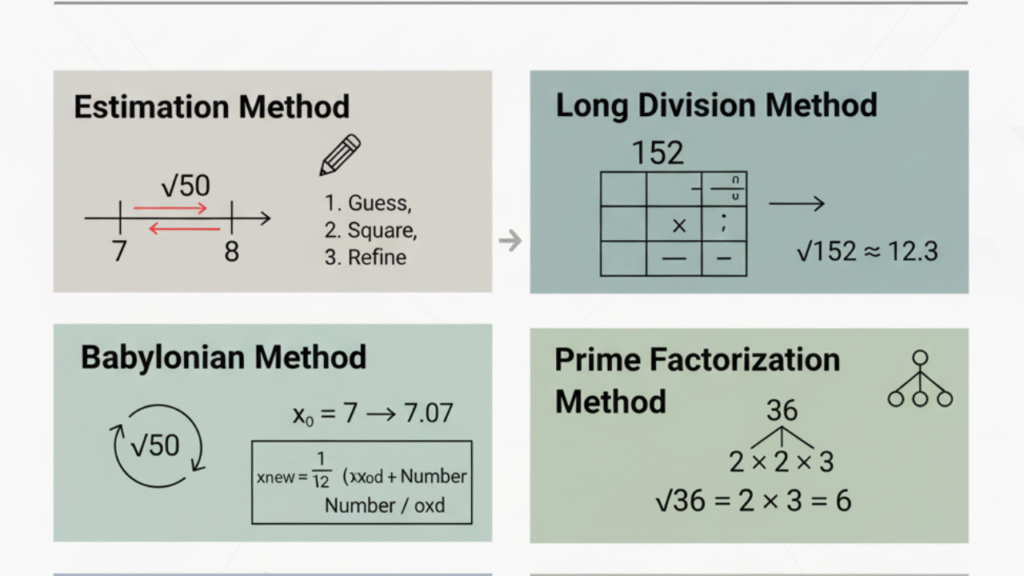
1. Estimation Method (Guess and Check)
This is the quickest and easiest method to estimate square roots without a calculator. It involves guessing a number and refining the guess based on how close the result is to the actual square root.
How to Estimate Square Roots Without a Calculator
Find Close Perfect Squares: To estimate √50, start by identifying the perfect squares around 50. We know that 72 = 49 and 82 = 64, so the square root of 50 is between 7 and 8.
Make a Guess: Start with the number 7, as it’s the closest to the answer.
Refine Your Guess: Try 7.1, since 7.12 = 50.41, which is very close to 50. Thus, √50 ≈ 7.1.
Example 2:
To estimate √200, we know that 142 = 196 and 152 = 225, so √200 is between 14 and 15. Start with 14 and refine your guess to 14.1 since 14.12 = 198.81, which is close enough to 200.
2. Long Division Method
The long division method is an efficient and accurate way to find the square roots of larger numbers. It’s similar to long division but with a few extra steps to help you calculate the square root.
Steps for Long Division to Find Square Roots
Group the Digits: For √152, group the digits as 1 and 52.
Estimate the First Digit: For 1, 12 = 1, so we start with 1.
Subtract and Bring Down: Subtract 1 from 1, then bring down the next pair (52).
Double the Estimate: Double the current estimate (1 becomes 2), and place this next to the remainder.
Refine the Guess: Keep adjusting and dividing the number by the new estimates until you reach your desired accuracy.
Example:
For √152, you’ll start with 1, subtract it, then bring down 52. You continue refining the estimate until you reach √152 ≈ 12.33.
3. The Babylonian Method (Heron’s Method)
The Babylonian method is one of the fastest ways to approximate square roots. It’s an iterative approach that quickly converges on the square root.
Steps for the Babylonian Method
Start with an Initial Guess: Let’s say we’re calculating √50, so start with x0 = 7, because 72 = 49, which is close to 50.
Use the Formula:xnew = 1/2 * (xold + (Number / xold))For x0 = 7:
x1 = 1/2 * (7 + 50 / 7) = 7.07
Repeat the Process: Keep refining your guess using the formula. After a few iterations, you’ll find √50 ≈ 7.071.
Example 2:
For √200, start with x0 = 14 (since 142 = 196), and apply the formula:
x1 = 1/2 * (14 + 200 / 14) = 14.14
Repeat the process to get closer to the true value.
4. Prime Factorization Method
For perfect square numbers, prime factorization is a quick and efficient method to find the square root.
Steps for Prime Factorization
Factor the Number: For 36, factor it into primes: 36 = 22 × 32.
Pair the Factors: For 36, the pairs are (2, 2) and (3, 3).
Take One from Each Pair: Multiply one number from each pair. So for √36, the result is 2 × 3 = 6.
Example 2:
For √144, factor it as 144 = 24 × 32, then pair the factors and multiply the square roots of each factor:
√144 = 2 × 2 × 3 = 12
5. Square Roots of Decimals
Finding square roots of decimals is similar to finding square roots of integers. You need to be careful when dealing with the decimal point.
Steps for Finding Square Roots of Decimals
Estimate: Start with a close guess. For √0.49, try 0.7, since 0.72 = 0.49.
Refine: Adjust your guess based on the result.
Example:
To find √0.25, start with 0.5, since 0.52 = 0.25.
Conclusion
Finding the square root without a calculator is possible and can be done with methods like estimation, long division, the Babylonian method, and prime factorization. Practice these techniques to improve your math skills and solve problems with confidence, whether you’re taking a test or just solving problems at home.
FAQs
Q: Can I find the square root of any number without a calculator?
Yes, you can find the square root of any positive number using these methods, whether it’s small, large, or a decimal.
Q: Which method is the fastest for approximating square roots?
The Babylonian method is the quickest and most accurate for finding square roots manually.
Q: How do I find square roots of decimals?
Use the same methods. Start with a close estimate and refine your guess.

